食品企業にとって、消費期限の延長はSDGsやフードロス削減の観点からも避けて通れない課題である。政府や業界団体からもフードロス削減に向けた具体的な指針が示される中、品質管理担当者は科学的なデータに基づいた厳密な判断を求められている。
しかし、測定結果には必ずばらつきが存在する。基準値をわずかに下回ったからといって、本当に安全と言えるのか。標準偏差、拡張不確かさ、相対標準不確かさ――これらを理解せずに基準値クリアを判断することは、消費期限の設定や延長において重大なリスクにつながりかねない。
本稿では、基準値判定における「測定の不確かさ」をどう捉えるべきかを解説し、平均、標準偏差、拡張不確かさ、相対標準不確かさといった基本概念をシンプルな事例で紹介する。さらに、消費期限設定への応用を視野に、現場で活用できる実践的な視点を提示する。
基準値をクリアした「はず」が、実は危うい──問題提起
たとえば、ある製品に対して「一般生菌数は3.4×10³ cfu/g以下であること」という基準値が設定されていたとしよう。
あなたの実験室で検査を行った結果は、3.3×10³ cfu/gであった。数字だけを見れば、基準値を下回っているため合格と判断したくなる。
しかし、ここで考えるべきなのが「測定の不確かさ」である。測定には必ずばらつきがあり、同じサンプルを繰り返し測定しても完全に同じ値が得られることはない。
仮にあなたの実験室のばらつきが極めて小さければ、3.3×10³という測定値をもって、「かなり確実に基準値を下回っている」と安心できるだろう。しかし、もしばらつきが大きかった場合、測定誤差の範囲によっては、実際には3.5×10³のような値に達してしまう可能性もある。
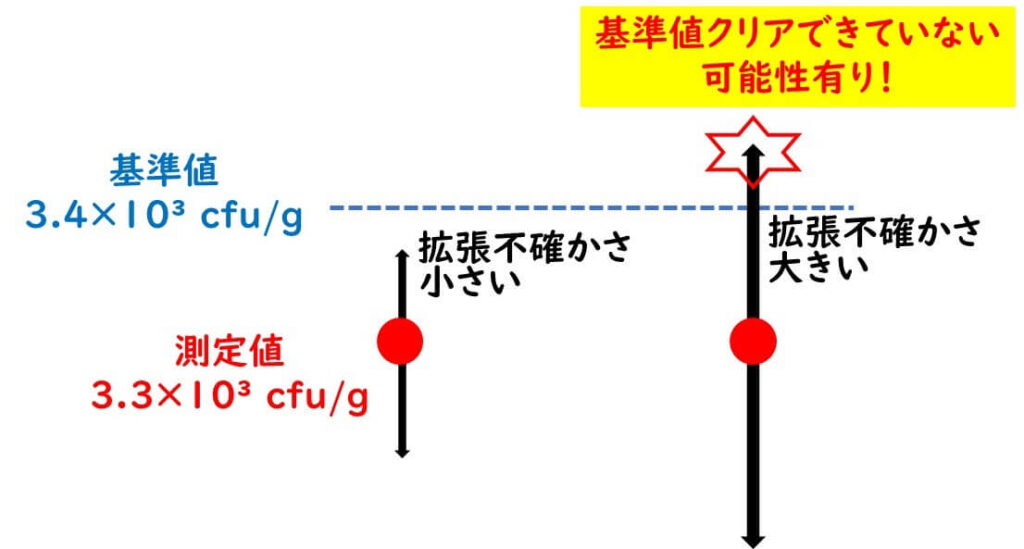
このようなズレが現実に起こり得るため、測定の不確かさをあらかじめ実験室として把握しておくことが重要なのである。
では、どのようにこの不確かさを把握し、判断に活かしていけばよいのだろうか。
測定値の不確かさを理解するための基本──平均・標準偏差・拡張不確かさ
不確かさを把握するには、まず基本となるいくつかの概念を押さえる必要がある。
1️⃣平均値を求める
平均値とは、複数回の測定結果をすべて足し合わせ、測定回数で割った値である。（この計算自体は、小学校で習う通りだ。）
ただし、微生物検査では注意が必要だ。
測定値は通常、対数変換（log値）した後の値で扱う。これは、生菌数のばらつきを安定させ、正規分布に近い形で評価できるようにするためである。
たとえば、測定値が「760 cfu/g」であった場合、これを常用対数（log10）変換すると、
log10(760)≈2.88
となる。
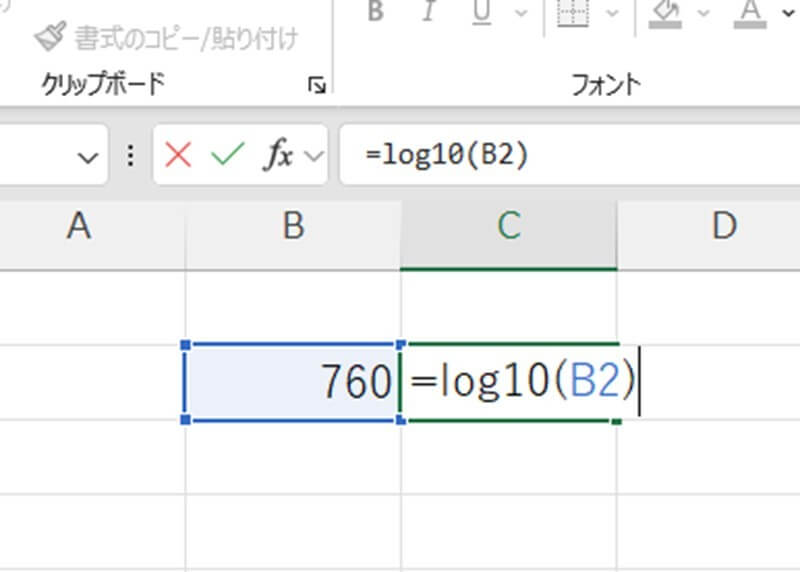
たとえば、同じサンプルを3人が測定し、対数値が2.4、2.45、2.30であった場合、この平均は (2.4 + 2.45 + 2.30) ÷ 3 = 2.383 となる。
2️⃣標準偏差（標本標準偏差）を求める
標準偏差とは、各データが平均値からどの程度ばらついているかを示す指標である。
標準偏差が小さければ測定のばらつきは小さく、大きければばらつきが大きいことを意味する。
具体例
たとえば、同じサンプルについて、3人の測定結果（対数値）が
- 2.4
- 2.45
- 2.30
だったとする。
標準偏差をエクセルで求める手順（ステップバイステップ）
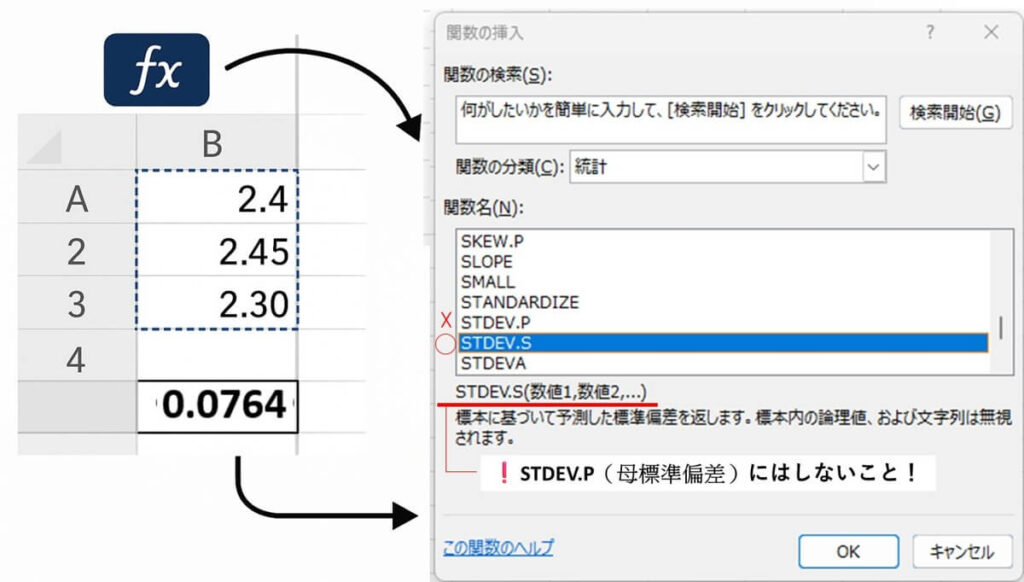
① 測定値をエクセルに入力する
- 任意の3つのセル（例：A1、A2、A3）に
2.4、2.45、2.30 を入力する。
② 標準偏差を求めるセルを選び、「fx」ボタンを押す
- セルを選択したら、エクセル画面上部にある fxボタン（関数の挿入）をクリックする。
③ 関数の分類を「統計」にする
- 「関数の分類」で「統計」を選ぶ。
④ 関数名から「STDEV.S」（標本標準偏差）を選ぶ
- 一覧の中から「STDEV.S」を選び、「OK」をクリックする。
ポイント：
- 関数「STDEV.S」は、標本標準偏差である。
- STDEV.P（母標準偏差）にはしないこと！
⑤ データ範囲を指定する
- 測定値が入力されている範囲（例：A1:A3）を指定して、「OK」。
ポイント：
- 手打ちで
=STDEV.S(A1:A3)と入力しても同じ結果が得られる。
⑥ 標準偏差が自動で表示される
- この例では、標準偏差（標本標準偏差、STDEV.S）は約0.076（log10）となる。
つまり、3人の測定結果のばらつきは「±0.076（log10）程度」というイメージになる。
標準偏差の計算方法と、STDEV.P（母標準偏差）にしてはいけない理由
標準偏差は「データが平均からどの程度ばらついているか」を示す指標である。数値的には、「平均との差の2乗を平均し、その平方根をとったもの」で計算される（つまり、全員のズレを計算して、その平均をとるイメージである）。
- 本来「平均」を計算するときはデータ数 N で割る。
- ところが、母集団すべてではなく、一部のサンプル（標本）だけで推定する場合には N−1 で割る。
こうすることで標準偏差は少し大きめに計算される。なぜなら、分母が小さくなる分だけ値が大きくなり、標本データの「過小評価しがちなばらつき」を補正できるからである。
- 母標準偏差（STDEV.P）：全部のデータがある(例：全社員の給与データ、1日の全測定値など） → N で割る
- 標本標準偏差（STDEV.S）：一部のデータで全体を推定する(品質管理での繰り返し測定、実験データ） → N−1 で割る
この補正により、少ないデータからでも全体のばらつきを妥当に推定できるようになる。食品微生物検査において測定不確かさを評価する際は、標本標準偏差（STDEV.S）を使用するのが原則である。母標準偏差(STDEV.P）で計算してしまうと、得られる標準偏差は真の値よりも小さくなってしまい、不確かさの評価を過小評価する可能性があるからである。
3️⃣拡張不確かさを求める
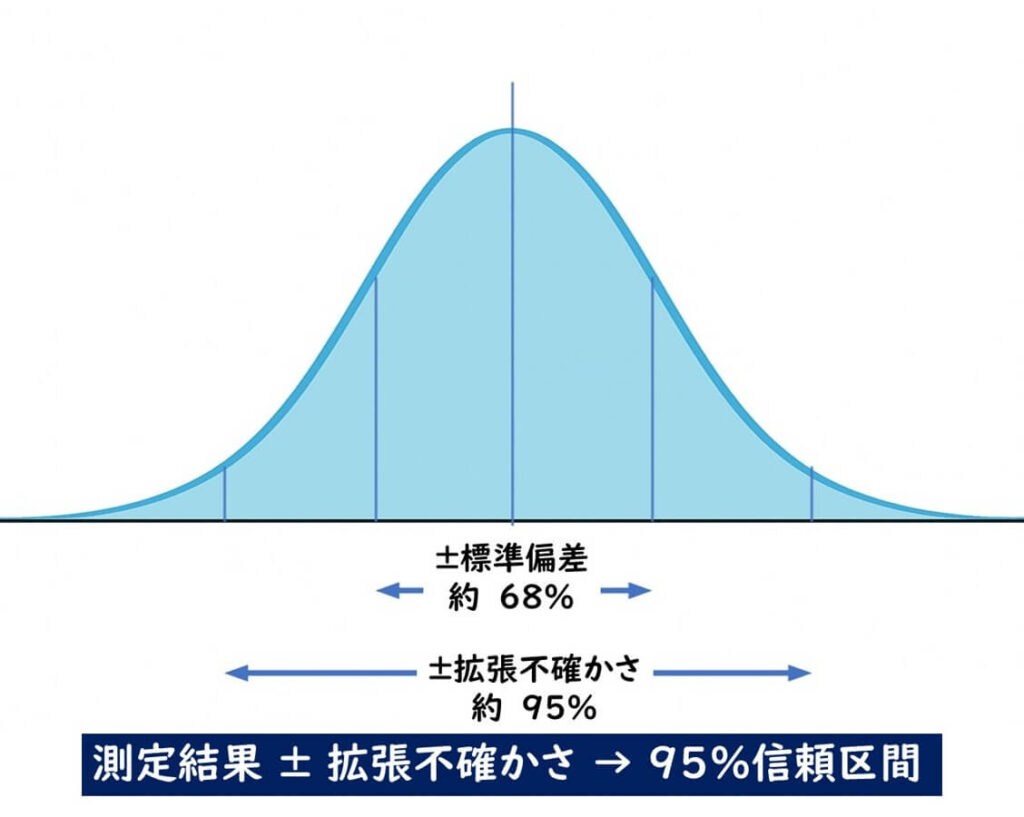
拡張不確かさとは、標準偏差（標本標準偏差）に信頼係数 k（通常2）を掛けたものである。
この「2」は、正規分布を仮定した場合に、測定値のおよそ95％がこの範囲内に収まることを意味する。
（参考までに、標準偏差だけでは約68％のデータしかカバーしない。）
理論的な定義
理論上は、拡張不確かさは次のように表される。
拡張不確かさ = 標準不確かさ（標準偏差 ÷ √n） × k（通常2）
ここでいう「標準不確かさ」とは、実際のデータのばらつきそのものではなく、より厳密には「平均値の不確かさ（= 真の平均〈母平均〉の推定誤差）」を指す。つまり、母平均をどれだけ正確に推定できるかを評価するための考え方である。
実務的な扱い（食品微生物検査の場合）
一方で、食品微生物検査の現場では事情が異なる。サンプリングや前処理の影響によるばらつきが支配的であり、母平均の精度を細かく評価するよりも、実際の測定値がどの程度ばらつくかを把握することが重要である。
そのため、実務では 標準偏差そのものを標準不確かさと見なし、さらに2を掛けて拡張不確かさを算出する方法 が広く用いられている。
計算例
標準偏差が0.076（log10）の場合、拡張不確かさは次のように計算される。
0.076 × 2 = 0.152
相対標準不確かさ──不確かさをパーセントで「見える化」する
さらに、拡張不確かさ（log10）を測定値（log10）で割ってパーセント表示することで、不確かさの大きさをより直感的に把握できる。
これが相対標準不確かさである。
たとえば、測定値の平均が2.383（log10）、拡張不確かさが0.15（log10）であった場合(※ここでは前セクションで求めた拡張不確かさ（0.152）を小数点2桁に丸め、0.15として計算）、
相対標準不確かさは
(0.15÷2.383)×100≈6.3%
となる。
相対標準不確かさは、菌数レベルが異なる検査対象を比較する際にも必須である。
たとえば、数千個の菌を測定する場合でも、数千万個の菌を測定する場合でも、絶対値だけを見て不確かさの大小を判断することはできない。なぜなら、絶対値（たとえば±0.15）は、測定対象の規模（ログ値の平均）が変われば、その意味がまったく異なってしまうからである。
今回例に挙げた測定では、対数平均2.383に対して拡張不確かさが±0.15であった。しかし、もし測定対象が対数平均5.0レベルの大規模な菌数だったとすれば、同じ±0.15の不確かさでは精度がまったく異なってしまう。
このように、相対標準不確かさをパーセントで示すことで、菌数規模に依存せず、不確かさの大きさを一貫した基準で正しく把握できるようになる。
注：ここでは log 値を使って相対標準不確かさを計算している。
元の cfu/g に換算してから求める方法もあり、どちらも正しい考え方である。
測定の不確かさを「使う」──実務への応用
では、これらの不確かさ情報を実際にどう使うのか、冒頭で提起したケースをもとに考えてみよう。
読者の実験室での測定結果は、3.3×10³ cfu/gであった。
一方、基準値は3.4×10³ cfu/g以下である。
ここで、読者のラボにおける相対標準不確かさが6.3%であるとわかっているとしよう(すなわち、日々の検査で生じるばらつきの大きさを代表する値として、相対標準不確かさ6.3%がすでに算出されていると仮定）。
この場合、拡張不確かさ（絶対値）は
3.3×103×6.3%≈0.208×103
となる。
つまり、測定値に対して±0.208×10³のばらつきがあると考えなければならない。
測定値±拡張不確かさを適用すると、
結果は次の範囲になる。
(3.092～3.508)×103
ここで注目すべきは、上限側が3.508×10³となる点だ。
基準値である3.4×10³を超えてしまう可能性があることがわかる。
つまり、測定結果そのものは基準値を下回っていても、
不確かさを考慮すると「超過のリスク」が現実に存在するのだ。
微生物検査の不確かさは「検査全体のトータル」で捉えるのが実務的
ISOや計量学に関する国際ガイドライン（たとえばISO『測定における不確かさの表現ガイド（GUM）』など）は、要因を分離して工程ごとに不確かさを評価できるならそうすべきとする。一方で、リスクに応じて評価の深さを合理的に調整し、まとめて扱うことも認めている。現実の検査現場でこれらすべてを厳密に分けて評価しているケースは多くない。これは微生物検査という領域の特性による。
微生物数の測定では、天秤の秤量誤差やピペットの分注誤差などの機械的な誤差に加え、サンプル中の微生物の分布が不均一であることが主要なばらつき要因となる。プレートカウントでは、分注・塗抹・培養条件の微妙な差が最終的な菌数に数倍の違いをもたらし得る。これは単なる操作ミスではなく、対象そのものの本質的ばらつきである。このため、各工程の個別誤差を理論どおりに分離・評価するよりも、「検査全体を通じたトータルのばらつき」として捉えるほうが、現場の実務に即している。
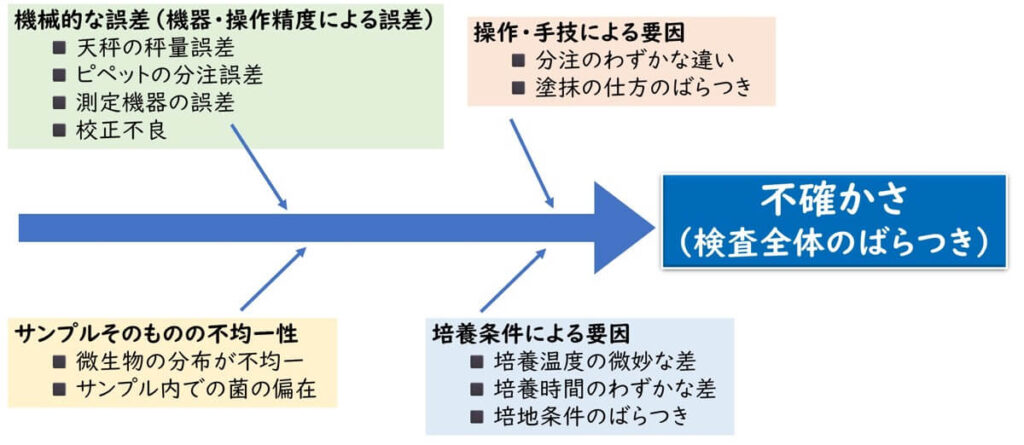
多くの検査室では、検査全体のばらつきをまとめて「測定の不確かさ」として管理しており、本稿でもその実務的な考え方に基づき、3名の検査員データというシンプルな枠組みで解説してきた。まずはこのアプローチを確実に身につけることが、実践的理解を深める第一歩である。
測定の不確かさは消費期限設定とリスク管理に直結する
不確かさの管理は理論演習ではない。消費期限設定をはじめ、企業の製品リスク管理に直結する。たとえば次のような判断は、不確かさの把握なしには成立しない。
- 保存試験で得られた生菌数データにどれほどばらつきがあるか
- そこからどれくらい安全マージン（0.7掛け、0.8掛けなど）を設定すべきか
検査データに内在するばらつきの大きさを把握せずに消費期限を設定することは、重大なリスクの見逃しに直結しかねない。測定の不確かさは、日々の検査業務を支えるだけでなく、製品安全性の担保や社会的信用の維持にも直接関与する。
本稿で示した基礎を、各社の保存試験設計・判定基準・安全マージン設定に体系的に反映してほしい。
