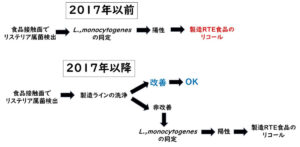
食品の安全性評価に不可欠な微生物濃度の精密推定は、統計学の力を借りて正確性を担保できる。特に、ランダムに発生する微生物の分布を予測するポアソン分布と、豊富なデータからの統計量を活用する対数正規分布の理解は、食品中の微生物濃度を正確に求める上で欠かせない。前記事でポアソン分布に基づく予測法を解説した。今回はデータが豊富な場合に適用される対数正規分布に焦点を当て、その使い方を解説する。この知識を武器に、微生物検査結果の解釈にに一層の厳密さを身に着けよう。
ポアソン分布予測の弱点
前記事で紹介したポアソン分布を前提として考える予測には一つ欠点がある。その欠点とはこうだ。ポアソン分布推計では電話の鳴る回数を推計する場合に、過去１日に 5回になるという平均値だけを用いて推計をした。ところが、たとえば次のようなケースはどうだろうか？
Aオフィス：過去100日間の一日あたりの電話の鳴る回数は5回になるが、毎日 4回から6回の間で確実に安定的に電話が鳴っている。いや、むしろ、ほとんどの日がぴったりと５回鳴る回数が圧倒的に多い。
Bオフィス：過去100日間の一日あたりの電話の鳴る回数は、１日 10回鳴る日もあれば0回しか鳴らない日もある。鳴る回数は不安定でランダムでであるが、とにかく最終的に平均をとると５回になる。
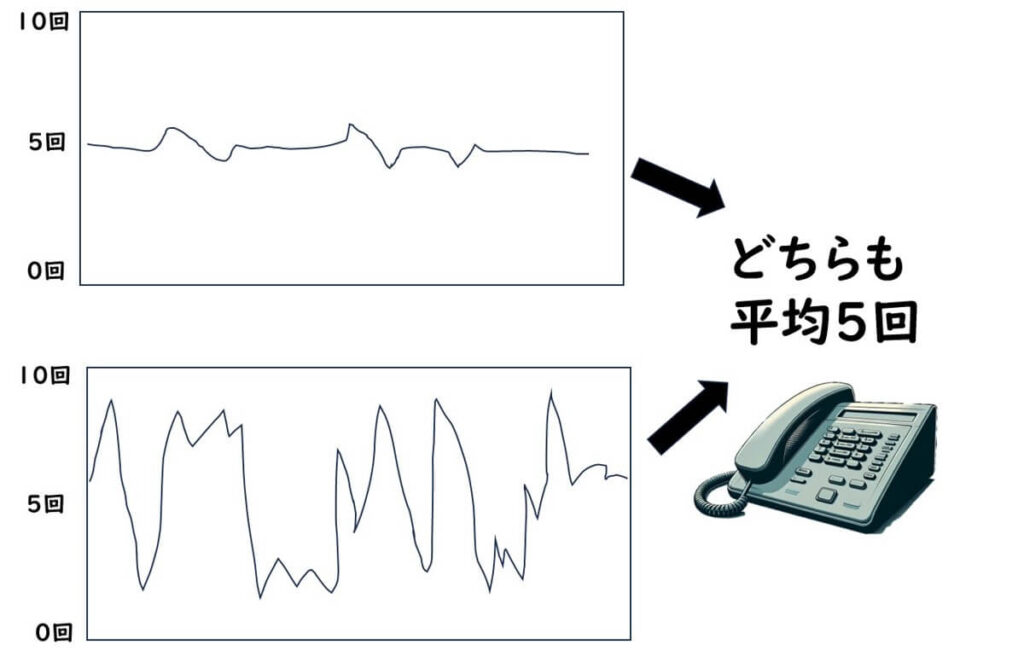
前記事で紹介したポアソン分布による推計は、あくまでも平均回数（５回）だけをもとに計算するやり方なので、AオフィスもBオフィスも、一日2回鳴る回数の推計は同じ推計（8.4%)になってしまう（計算法は前記事参照）。しかし、Aオフィスでは、過去100日間でに電話が２回しか鳴らなかったことは一度もない。つまり、この推計確率は過大推計なってしまう。
つまりポアソン分布による推計はBオフィスでは適しているが、Aオフィスの場合は必ずしも的していないということになる。
したがって、食品産業において微生物濃度を正確に評価するためには、豊富なデータがあり、特にデータの分布が対数正規分布に従うと予測される場合は、対数正規分布と標準偏差を用いることでより正確な結果を得られる。
試験の合格点予測
微生物の定性試験から菌数予測の式を説明する前に、もう少し簡単な例え話で進めることにする。現在、山田君と鈴木さん、どちらも食品会社に勤めているが、ある食品微生物の資格試験を受験したとする。受験者は1000人だ。合格定員は100人だ。
2人は受験をして、受験後に試験主催者から公表される合格、受験者の平均点（59点）と標準偏差（9点）だけが公表された。
山田君の自己採点は70点、鈴木さんの自己採点は72点だった。2人とも、この受験者の平均点59点ということから、自分たちが10%の中に入るかどうかを知りたがっている。これを正確に予測することによって、2人は心置きなくヨーロッパ旅行へ出かけられるのだが、試験の合格発表日は一ヶ月先である。そこで合否を予測したいと考えている。
統計計算につよい社内の田中さんに聞いてみたところ、残念ながら山田君は不合格、鈴木さんは合格とのことだった。
どうしてこのような計算ができるのかというと、田中さんは、これは
平均と標準偏差に対する正規分布の 累積分布関数の逆関数（NORMINV 関数）によってできるということだった。その結果、上位10%に相当する得点は71点になるとのことだった。
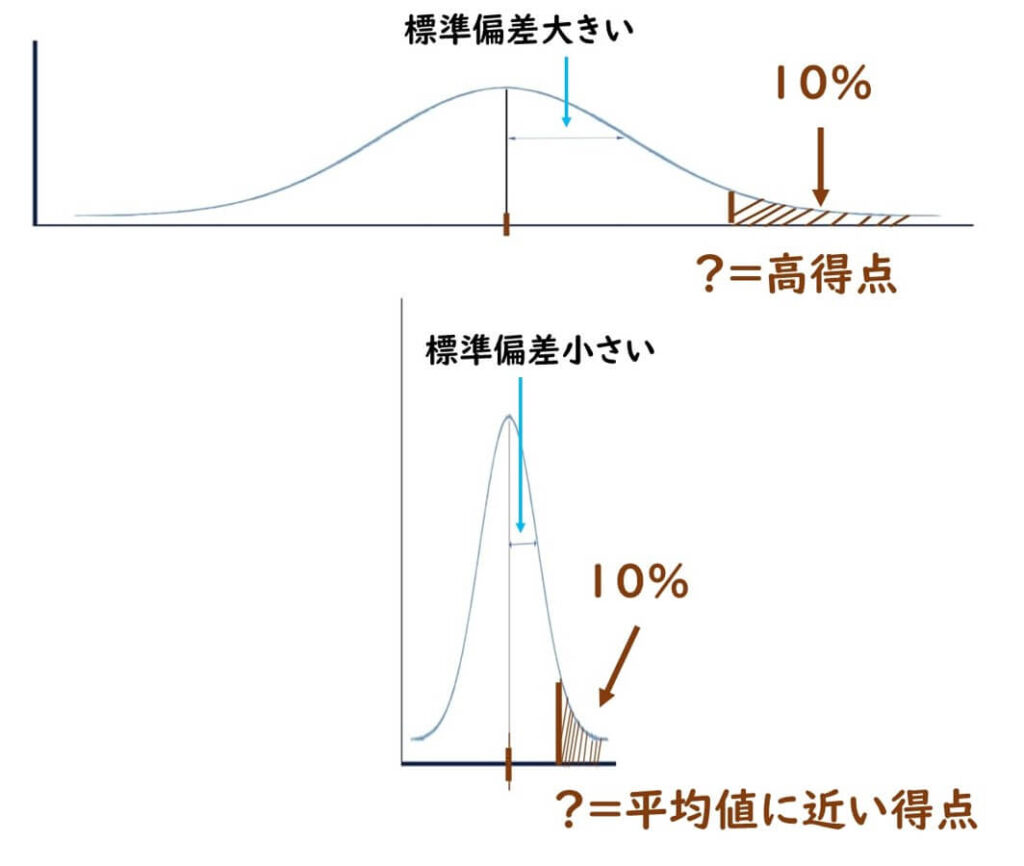
ここで読者は平均と【標準偏差に対する正規分布の 累積分布関数の逆関数】という難しい言葉を聞いて、これ以上先を読む興味を失うかもしれない。しかし、実際はこの計算の意味自体は非常にシンプルだ。下の図を見てほしい。これが今回の受験者の得点分布だ。一般的に受験者の特定分布はこのような対数正規分布となる。そして、真ん中の山の頂上が平均点、すなわち59点である。ここで合格者は上位10%なので、このグラフの右側の10%のところの点数を予測すればいい。
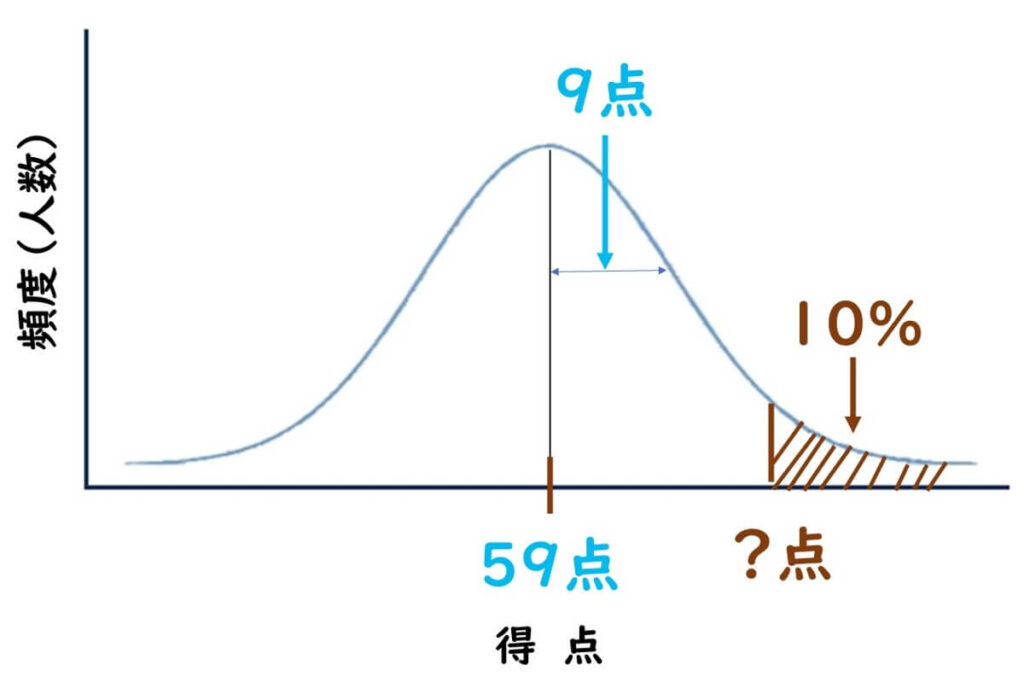
ただし、この山の形が非常に険しい場合と、緩やかな場合とで点数予測は当然異なる。そこで、この山の形の険しさを決定するのが標準偏差注）だ。標準偏差とは、要するに平均点からどれぐらいばらつきがあるか、この場合の山で言えば山が非常にシャープであるか緩やかであるかということだ。標準偏差が小さければ、山は極めて険しい。標準偏差が大きければ、山は極めてなだらかである。
注）標準偏差を計算する方法
- 平均値を求める: まず、全てのデータの平均値を計算する。例えば、5人のテストの点数が50点、60点、70点、80点、90点なら、その平均値は(50+60+70+80+90)÷5 = 70点になる。
- 差の二乗を求める: 次に、各データが平均値からどれだけ離れているかを計算する。しかし、単純に差を求めるとプラスマイナスが相殺されてしまうので、差の二乗を求める。つまり、(50-70)²、(60-70)²、(70-70)²、(80-70)²、(90-70)²と計算する。
- 差の二乗の平均を求める: これら差の二乗の平均値を計算する。これが分散になる。
- 平方根を取る: 最後に、分散の平方根を計算する。これが標準偏差である
ここでは標準偏差が7点ということなので、平均点からだいたい得点者のばらつきが平均するとだいたい7点プラスにもマイナスにも7点触れているということだ。一般的にこれは平均の偏差なので、その大体7×2の14点ぐらいの上下±をすると、受験者95％の点数が入るという仕組みだ。いずれにしても、ここで与えられているのは
- 平均点（＝59点）
- 標準偏差（＝9点）
- 全体の10%
という3つの数字だけだ。これらの数字から、上位10%の点数を予測する。これが標準偏差に対する正規分布の 累積分布関数の逆関数ということだ。
この計算は複雑なアルゴリズムを要するため、Excelに頼るのが最適だ。本記事では、Excelでの入力方法に焦点を当てる。以下の式をExcelのセルに入力する：
=NORM.INV(確率, 平均, 標準偏差)
このケースの場合、下記のように入力する。
=NORM.INV(0.9, 59, ９)
ここで、0.9は上位10%を意味する逆の確率（つまり、90%）である。次に、平均値を中央に、標準偏差を最も右に配置する。この式により、上位10%の得点を簡単に計算できる。
なぜ確率に0.9を使用するのかという疑問に対しては、この関数で必要とされるのは、求めたいスコアが下回る全体の累積確率だからだ。例えば、上位10%のスコアを求めたい場合、それは全体の90%がそのスコア以下であることを意味するため、確率として0.9を用いる。
対数正規分布と標準偏差からの微生物菌数予測
ここまでで、勘の鋭い読者はすでに微生物の定性結果から菌数を予測する方法のヒントが浮かんだかもしれない。
実は定性試験の結果から微生物の菌数予測は前の節で説明した平均点と標準偏差から合格点を計算する方法と、全く同じやり方で算出することができるのだ。
下の図をご覧いただきたい。現在、微生物の定性検査における陽性率が10%だとする。ここでの陽性か陰性かの判定は、試料25gを用いた増菌培養の結果に基づく。一般的に、食中毒菌の定性検査では食品試料25gを増菌培養液225mlで希釈して増菌する。この場合、検出限界は１cfu/25g = 0.04cfu/gとなる。
下の図をご覧いただきたい。現在、微生物の定性検査における陽性率が10%だとする。ここでの陽性か陰性かの判定は、試料25gを用いた増菌培養の結果に基づく。一般的に、食中毒菌の定性検査では食品試料25gを増菌培養液225mlで希釈して増菌する。この場合、検出限界は１cfu/25g = 0.04cfu/gとなる。
この値を対数（log10）に変換すると、-1.3979になる。
また、過去の食中毒菌の検出結果や分布の分析に基づき、対数正規分布における対数値（log10）の標準偏差を0.8と仮定する。この値は、大腸菌やサルモネラ菌など多くの研究対象で採用されており、食品検査における標準的な仮定とされている。
ここでの目的は、下図の左側に描かれている山の頂点、つまり未知の微生物の濃度を予測することだ。これは、以前の点数予測と非常に似ている。異なる点は、以前の予測では平均点が既知であり、10%の部分の点数を求める式であったのに対し、今回は平均点が不明で、逆に10%の部分、すなわち微生物濃度が0.04CFU/gとして既知（25g試料の定性検査での陽性判定の検出限界、1/25=0.04）だ。求める方向が逆であることを除けば、同様のExcelの計算式を使用すれば求めることが可能だ。
この値を対数（log10）に変換すると、-1.3979になる。
また、過去の食中毒菌の検出結果や分布から、対数正規分布における対数値（log10）の標準偏差を0.8と仮定する。標準偏差の設定は、過去の試料中の食中毒の分布パターンを基に判断される。
ここでの目的は、下図の左側に描かれている山の頂点、つまり未知の微生物の濃度を予測することだ。これは、以前の点数予測と非常に似ている。異なる点は、以前の予測では平均点が既知であり、10%の部分の点数を求める式であったのに対し、今回は平均点が不明で、逆に10%の部分、すなわち微生物濃度が0.04CFU/gとして既知（25g試料の定性検査での陽性判定の検出限界、1/25=0.04）だ。求める方向が逆であることを除けば、同様のExcelの計算式を使用すれば求めることが可能だ。
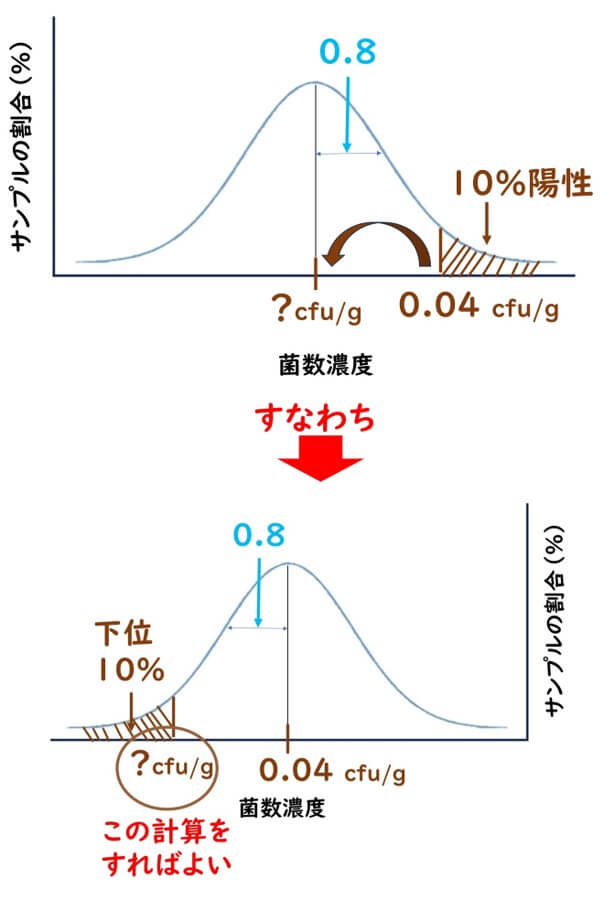
上図のように、要するに、平均菌数濃度が0.04cfu/gの微生物集団があり、下位10%（上位90%)に相当する濃度を求めれば良いということになる。
求める菌数濃度＝NORM.INV(0.1※、平均（対数）、標準偏差（対数））
※資格試験の場合は上位10%の場合、 0.9を代入したが、今回はそもそも正規分布グラフを上に説明したように逆反転させて考えているので、このまま微生物定性検査の陽性率の数字をそのまま入れる。
では、実際にEXCELで計算をやってみよう。
下表に示された条件で、サンプル数が30で、それぞれのサンプルでの陽性数が15、5、25の場合の菌数予測を計算する。標準偏差は対数(log10)で0.8とする。資格試験の点数予測と同様の方法で計算を行う。つまり、
求める菌数濃度＝NORM.INV(陽性率、平均（対数）、標準偏差（対数））
という式を使用する。
具体的なExcelでの入力例は以下の通りだ。
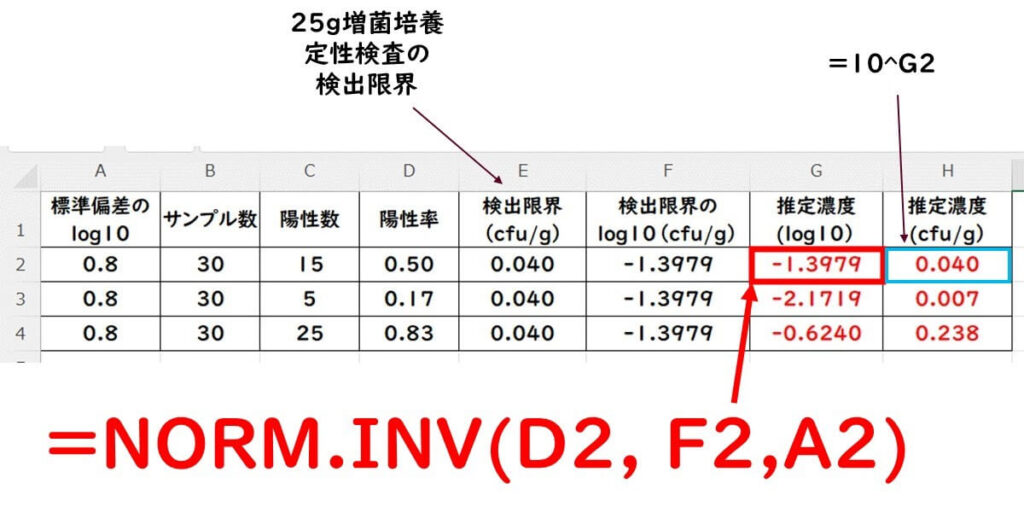
この例では標準偏差を0.8としたが、さまざまな標準偏差を試すことでさまざまな濃度を計算できる。この点については、文字で説明すると複雑になりすぎるため、ビデオで説明している。
まとめ
今回は微生物の定性試験から菌数を予測する際に、対数正規分布を前提とし、さらに標準偏差を設定することの意義を紹介した。前回の記事で取り上げたポアソン分布の手法は、平均値を基にした品質結果の修正のみを提供し、データのばらつき（分布の幅や標準偏差）は考慮できないため、データが少ない場合の簡易的な方法として利用される。
一方で、今回紹介した対数正規分布を用いた方法は、事前にデータが集約されており、サンプル間での微生物菌数のばらつき（標準偏差）がある程度分かっている場合に有効である。このアプローチは、ICMSF（International Commission on Microbiological Specifications for Foods）が食品の微生物規格やリスク評価で推奨している考え方とも一致しており、信頼性の高い推計手法の一つである。
ただし、これら二つの方法は、推測に過ぎないことを理解する必要がある。すべての統計予測に共通して言えることだが、絶対的に正しい予測というものは存在しない。手持ちのデータ、すなわち定性試験の陽性率や微生物の検出限界（例えば、0.04CFU/g）だけに基づいて予測しているに過ぎない。直感に頼ることも、場合によっては正解かもしれないが、その場合、予測は人や状況によって変わるため、一定の計算ルールに従って予測を行うべきだ。しかし、この計算ルールが絶対的に正しいわけではないこと、あくまで一つのルールに基づいた予測であることを念頭に置くべきだ。異なる日や異なる人々が同じデータに基づいて予測を行った場合、共通の理解としてこの前提に基づいて行ったと説明できるようにするためだ。決してこの予測が正しいとは限らないことを留意する必要がある。
ICMSFの考え方も含めて、これらの推計手法は、あくまで、食品安全性評価を統一的に行うためのの一助であり、完全な答えではないことを念頭に置きつつ、最善の判断材料として活用するべきである。
