微生物の定性検査結果から菌数を推測①-ポアソン分布公式でやてみよう

　食品の品質管理には、初期の微生物数を正確に把握することが不可欠である。食中毒菌の濃度をどのように推測するかは、食品の安全性と消費期限の設定に直結する。この記事では、定量法が困難な場合でも、定性検査の結果を基に菌数濃度を見積もる統計的アプローチについて、数的処理が苦手な人でもわかるように解説する。具体的には、ポアソン分布を用いたアプローチと、対数正規分布を利用し標準偏差を考慮したアプローチの二つを紹介する。本シリーズの初回では、ポアソン分布に基づく推計法に焦点を当てる。

はじめに

　　この記事では、食品の微生物検査における重要なプロセスである定性検査と、その結果をもとに菌数濃度を推計する方法に焦点を当てる。定性検査とは、25gのサンプルから微生物の存在を陽性または陰性で判断する、日常的な食中毒菌の検査プロセスである。この検査により、菌の存在有無は判明するが、具体的な菌数を知ることは通常できない。

　食品の消費期限やHACCPでのCCP設定においては、食品中の食中毒菌の具体的な数の把握が重要である。一般的に、平板混和法やMPN法により、一般生菌数を定量的に測定することが基本であるが、食中毒菌の分布は非常に不均一であり、通常は検出されにくく、稀に検出されることもある。このため、定量実験の実施は困難であり、結果の信頼性も低いことが多い。

　その解決策として、25gのサンプルを用いた定性試験の結果から統計的に菌数を推計する方法が有効である。この方法により、日常的な検査データを利用して、菌数濃度を定量的に推計することが可能となる。この記事では、その具体的な方法と、統計的シミュレーション手法を用いたアプローチについて解説する。

　多くの食品微生物の品質管理担当者が数学的な統計処理を苦手としている人も多いと思うので、この記事は数的処理が苦手な人でも理解しやすいように構成されている。数学や統計が専門でない初心者向けに、菌数の推計方法を分かりやすく説明することが目的である。

　この記事は三部構成で進められる。読者のニーズに応じて、第一節のみを読むこともできるし、興味があれば第二節や第三節もお読みいただきたい。

　第一節では、25gのサンプルに基づく定性検査の結果から、存在する菌数をどれくらい求めるかについての具体的な方法のみを説明する。細かい理論や計算を抜きにして、とりあえず、定性試験の結果から菌数濃度を推定するという、実践手順ことに焦点を当てる。EXCELシートも使うので、一部ビデオの説明も取り入れることとする。

　第二節は、検査方法だけでなく、その背後の考え方や理論的背景に興味を持つ読者向けにする。ポアソン分布の公式（電話の鳴る回数予測）が登場する。ここでは、統計的シミュレーションの式が持つ意味と、それがどのような観点から作られたかをわかりやすく説明する。

　第三節は、用いられる式の具体的な式変換処理について解説する。この部分では、高校数学レベルの数式の扱い方を用いて補足的に説明する。

　この記事で紹介される菌数濃度の測定方法は、以下の論文で用いられている方法に基づいている。菌数濃度を測定するには他にも方法が存在するが、ここでは特に初心者にも理解しやすい下記の論文のアプローチを紹介する。

Valero et al.
Probabilistic approach for determining Salmonella spp. and L. monocytogenes concentration in pork meat from presence/absence microbiological data
International Journal of Food MicrobiologyVolume 184, 1 August 2014, Pages 60-63

第1節：とにかく定性結果から菌数濃度を出してみよう

まず結論から始めることにしよう。以下の式を用いることで、食品中の微生物濃度が求められる。

λ=− ln(1−p)/0.025

　ここで、λは求めたい微生物の濃度である。ただし、この場合はキログラム当たりのcfuで表される。微生物学ではグラム単位が一般的であるが、統計的な解釈を一致させるために、キログラム単位で表されることが多いので、まずはキログラム単位であることを理解してほしい。例えば、73cfu/kgのように結果が表される。

　pはサンプルの陽性率を表す。例えば、25サンプルを分析して5サンプルが陽性の場合、5/25 = 0.2となる。

　0.025は、25gのサンプルを1キログラムに換算したものである。

　lnは自然対数で、特別な数である「ネイピア数 e」（約2.718）を基準とした対数を指す。対数とは、「ある数 x が e を何回掛け合わせたものか」を表す計算である。自然対数は、成長や減少など自然界で起こる多くの現象を説明するのに役立つ。「ln x」はネイピア数 e＝約2.718を何乗したら x になるかを求める計算である。λとpについての説明は理解できても、lnやネイピア数 e の説明になると、読者の多くが混乱するかもしれない。初心者は、lnとネイピア数 e が何かについて心配する必要はない（ネイピア数とはなにかについては、本節の末尾に注釈した）。まず第一節では、この式を実際にエクセルで入力し、定性検査の結果から濃度を実際に求める具体的な方法だけを理解しよう。

　上記式をExcelシートに入力して求めればよい。この数式は、微生物のサンプル中の分布がポアソン分布に従うという前提で作られている。微生物の分布パターンについて、食品サンプル中のサルモネラなど確率的に頻度が少ない場合、ポアソン分布を用いる方が適切とされている。

ポアソン分布って何？

ポアソン分布についての解説は第２節で説明するが、第１節ではまずは、この式を運用することのみに集中する。

Excelシートで濃度 λ を計算するためには、以下のような式をセルに入力する。

• Aのカラムに分析サンプル数を入力
• Bのカラムに陽性サンプル数を入力
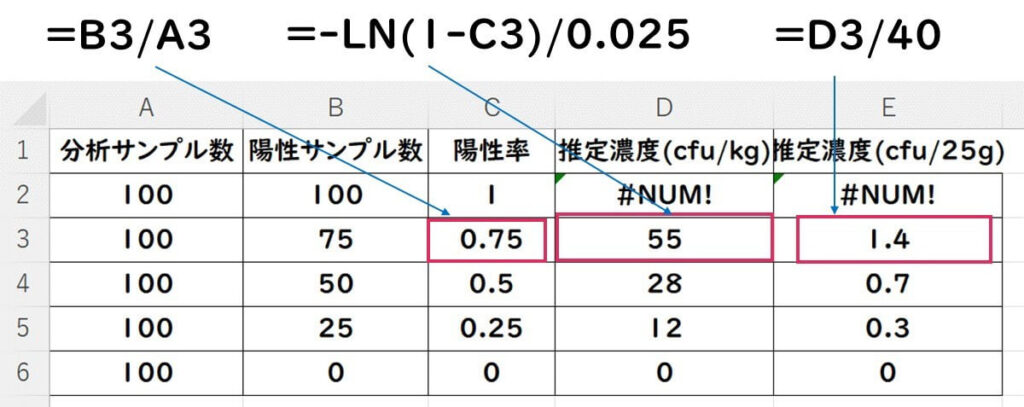
• Cのカラムに陽性率の欄を設定し=Aカラム/Bカラムを入力（行に応じて、例えば=B3/A3など）
• Dのカラムに推定濃度λの欄を設定し、=-LN(1-C3)/0.025　を入力。ここで、LN は自然対数lnを計算するExcelの関数である。Excelで自然対数を計算する関数 LN を使用する際には、アルファベットの大文字「L」と「N」を入力しても問題ない。Excelの関数は大文字と小文字を区別しないため、LN、Ln、または ln のいずれの書き方でも同じ関数として認識される。したがって、セルに =-LN(1-C3)/0.025 と直接、手入力するだけで正しく計算が行われる。Excel計算は、まず、LN(1-C3)を計算し、それを0.025で割って、さらにマイナスをつける順で実行される。とにかく、Excelの数式バーにこの式を入力し、Enterキーを押すと計算結果が表示される。Excelの関数メニューから探して挿入する必要はない。直接セルに式を入力するだけで大丈夫である。
• Eのカラムに25g単位の濃度を計算する。Dのカラムで求めた濃度（cfu/kg）を40で割り、Eのカラムに25g単位の濃度（cfu/25g）を計算する。セルに以下の式を入力：=D3/40 　　

　以上で、Excelシートセルに と直接入力するだけで、正しく微生物菌数濃度計算が行われる。

　Excelシートに式を入力して解を求める方法は、以上のような文章での説明に加えて、動画を用いた説明がわかりやすいだろう。このため、この部分については動画も追加することにした。以下のリンクから動画をご覧いただきたい。

https://youtu.be/sv0-lK8DOC4

注）ネイピア数を理解するには、複利計算の概念を考えると良い。元本が年率100%の利息で複利計算される場合、利息が年に1回付けられるならば、1年後の元本は2倍になる。しかし、利息が半年に1回付けられるとすると、1年後の元本は(1+1/2)²=2.25=2.25倍になる。この利息の付け方を無限に細かくしていくと、つまり1年を通じて継続的に利息が複合されると、元本の増加率はネイピア数に収束する。17世紀にスイスの数学者ヤコブ・ベルヌーイが複利計算を研究している中で、ネイピア数が自然成長のプロセスを表すのに適していることを発見した。ネイピア数は、自然界の成長プロセスや物理現象を記述するのに非常に便利な数であり、微分積分学の発展とともに、科学や工学の多くの分野で広く利用されている。初心者は以上の概略理解でよいだろう。とりあえず、この便利な数字ネイピア数 e＝約2.718とだけ、理解しておけばよいだろう。

第２節：式の意味の理解

　さて、この節では、第一節で用いたExcel用の入力式、つまり下記の式が、どのような意味をもって、なぜこのような式が作られたのかについてを理解していただくために以下説明をする。

λ=− ln(1−p)/0.025 ・・式A

　この式はもともと下記の式Bをλ=で立て直したものである。

p=1−e^{(−λ×0.025)}　・・式B

　式Bのλ（ラムダ）はサンプル中の微生物の平均濃度（cfu/kg、つまり1キログラムあたりの微生物のcfu）を表し、サンプルサイズ（25g = 0.025 kg）を乗じている。式Bから式Aの変換方法は、第３節で説明する。

　本節の目的は式Bの意味を説明することである。この式を理解するためには、ポアソン分布の基本的な理解が必要になる。難しく感じるかもしれないが、要するにポアソン分布というのは、「ある時間内に特定の事が何回起こるか」を表す分布で、例えば1時間に何回電話が鳴るかのような事象に使われる。まずは基本的な例題で説明する。

過去平均１時間5回鳴っていたオフィスで、次の１時間に電話が２回鳴る確率（ ポアソン分布公式）

例題：　今、ある営業所で一時間当たり平均5回電話が鳴っているとしよう。これはあくまでも平均であり、一時間当たり１回しか鳴らない場合もあれば、6回鳴る場合もあるし、2回鳴る場合もある。これらの平均をとると一時間当たり5回に鳴っていると言うことである。では、これから１時間で２回鳴る確率はどうなのか？というような確率を計算するのがポアソン分布の確率の基礎計算である。

単位時間当たり平均λ回起こる事象が、つぎの単位時間でk回起きる確率P(x=k ）を求める公式は以下のとおりとなる。

P(x=k ）=(λ^k ・e^-λ)/k!

「 e」はネイピア数 で約2.718である。

！は、例えば5！というのは5×4×3×2×1を計算するという意味である。

　この公式がポアソン分布公式である。この公式は電話の鳴る回数や不良品の発生回数など、多様な場面で応用可能であり、便利である。本記事はポアソン分布の公式が、なぜこの式になるのかについては説明しない。本記事はあくまでも食品微生物学を学ぶ者で算数の苦手な方向けなので、まずはこの公式を覚えることで割り切ろう。なお、この導出理由も理解したい方は、本式はポアソン分布の定番なのでネット等で調べ、学習することを勧める。

では、さっそく、この公式を用いて、１時間で２回鳴る確率を計算してみよう。λ＝５、k=2を代入するだけでよい

P(x=2）=(5² ・e^-5)/2!=

を計算すればよい。手計算では無理なのでExcelシートを使おう。以下のような式をセルに入力する。

• Aのカラムに平均回数λを入力（今回の計算の場合すべて５）
• Bのカラムに起きる確率を調べたい電話の回数ｋを入力
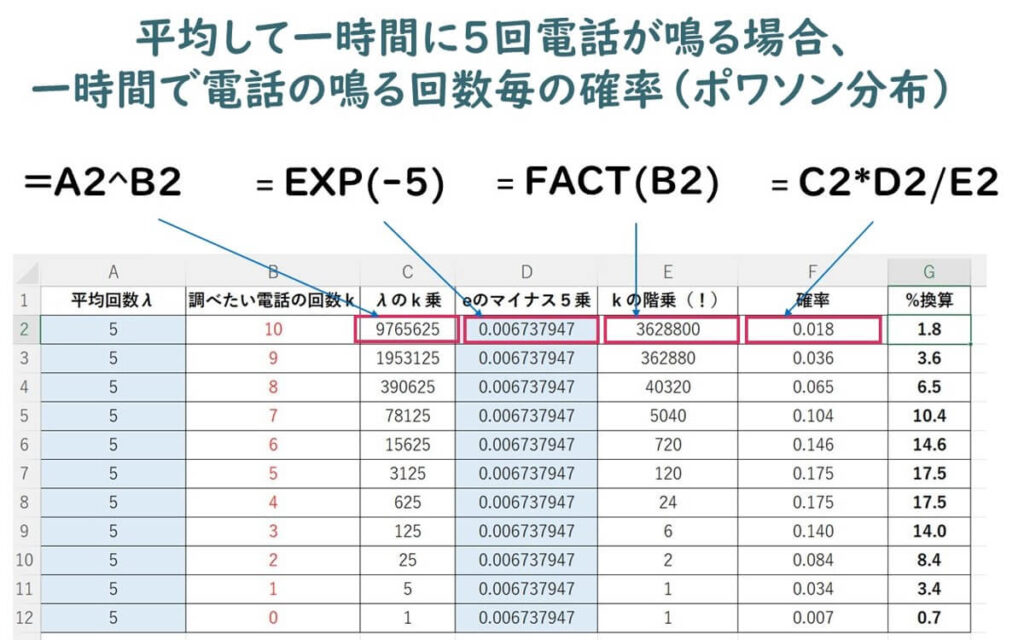
• Cのカラムにλのｋ乗を入力（行に応じて、例えば=A2^B2）（^は、キーボードの「ほ」の右のキー）
• Dのカラムにeのマイナス５乗を入力（すべての行一律に、=EXP(-5)を入力すればよい）
• Eのカラムにｋの階乗（！）を入力（行に応じて、例えば=FACT(B2)）（FACTはExcelの階乗計算コマンド）
• Fのカラムで求めたい確率がでる（行に応じて、例えば=C2*D2/E2）
• Gのカラムで％換算の確率にすればわかりやすい

Excelシートの入力方法は下記のとうりである。

１時間で２回鳴る確率は、8.4%であることが計算でわかる

　上記のエクセルシートの電話回数を横軸、その確率を縦軸に取ったグラフが下の図である。ポアソン分布はこのような典型的なグラフパターンとる。ただし、あくまでも分布は連続性ではないので棒グラフになる。

　

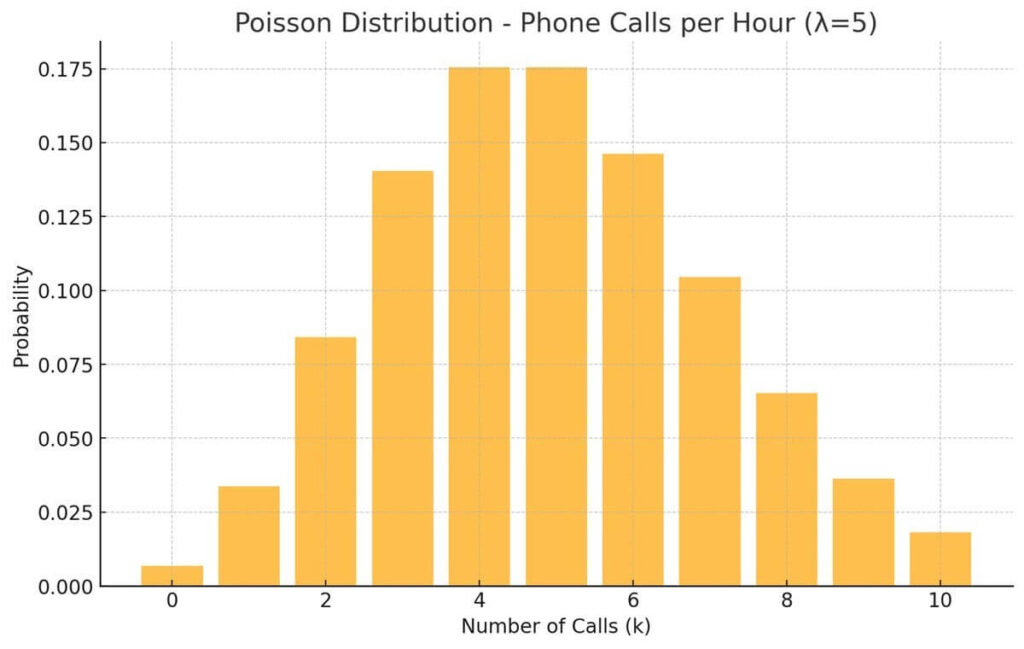
ポアソン分布公式を微生物の濃度計算に応用する

以上、電話回数のポアソン分布計算の基礎がわかったうえで、いよいよ本題に入る。

　　電話が0回になる確率を見てみよう。上のエクセル表では、丸めて0.007としているが、正確には、0.006737947である。つまり、ということは、つまりDのカラムにeのマイナス５乗と同一となる。なぜか？

P(x=0）=(5⁰ ・e^-5)/0!=

の計算となるのだが、ここで、5⁰＝１となり、また、0!=１となる（以上は、数学の決まり）

P(x=0）=(5⁰ ・e^-5)/0!=(1 ・e^-5)/1=e^-5となるわけだ。

つまり、

０回鳴る確率 p=e^-5

０回鳴る確率と、１度も鳴らない確率は、同義なので、

すなわち

１度も鳴らない確率 p=e^-5

となる。

さて、ここで、微生物の上記公式にもどろう。

p=1−e^{(−λ×0.025)}　・・式B

e^{(−λ×0.025)}に注目していただきたい。式Bのλ（ラムダ）はサンプル中の微生物の平均濃度（cfu/kg、つまり1キログラムあたりの微生物のcfu数）を表し、サンプルサイズ（25g = 0.025 kg）を乗じている。つまり、λ×0.025＝25gあたりのcfuである。

　さて、重要なポイントは、上で説明した一時間当たりの平均電話回数を、ここでは25gあたりの平均cfuに置き換えていることだ。電話の回数であれ、微生物の濃度であれ、時折しか起きない事象の平均（電話の場合は鳴る回数、微生物の場合は25gあたりのCFU）は同一である。この理解ができれば、後は容易である。

つまり、

e^{(−λ×0.025)}：25gあたりのCFUが一度も検出されない確率
（電話が一度も鳴らない確率に相当）

となる。

　ここで電話の場合でもう一度考えてもらいたいが、電話が一度もならない確率を１から引くとどうなるか？これは少なくとも１回以上になる確率（電話の回数は問わない）ということになる。

　微生物の場合も同様で、一度も検出されない確率を一から引くと、少なくとも一度は検出される確率ということになる。

すなわち、p=1−e^{(−λ×0.025)}　・・式Bは、何を意味するかというと、１からe^{(−λ×0.025)}を引いているので

p=25g検査で少なくとも１度は陽性になる確率となる。

確率と頻度の関係: 確率は、ある事象が発生する期待頻度を示している。したがって、実際の検査で得られた陽性の頻度（陽性率）は、その事象の発生確率を示唆していると解釈される。つまり、

p=25g検査で少なくとも１度は陽性になる確率＝実際の定性試験の検査結果（陽性率）

　さて、この記事のテーマは日常的な25gあたりの定性試験の結果から微生物の菌数濃度を推定しようというものだったことをここで思い出そう。

つまりp=1−e^{(−λ×0.025)}　・・式Bの意味は、

定性試験の陽性率^注）=1−e^{(−λ×0.025)}

注：たとえば、100サンプルで25サンプル陽性なら0.25

となる。このように、微生物の定性試験の結果と微生物の平均濃度、^λとの関係式が式Bということになる。

第３節：式の解法

　最後に、この節では、式Bから式Aを求めるステップを説明する。

p=1−e^{(−λ×0.025)}　・・式B

λ=− ln(1−p)/0.025 ・・式A

この式をλ＝の形にしてみよう。

• 1を左辺に移します p-1=-e⁡^{(−λ×0.025)}
• 両辺にマイナスをかける　 1-p=e⁡^{(−λ×0.025)}
• 次に、両辺の自然対数（ln）を取る。ln(1−p)=ln(e⁡^{(−λ×0.025)})
• そもそもの自然対数（ln）の定義上、ln(e⁡^{(−λ×0.025)})は、⁡−λ×0.025となる。したがって、ln(1−p)=⁡−λ×0.025
• 最後に、式をλについて解く。これを行うために、両辺を-0.025で割る。− ln(1−p)/0.025=λ
• 左辺と右辺を逆表記するとλ=− ln(1−p)/0.025

以上、➎は式Aであることがわかる。

まとめ

　本記事では、食品中菌の定性試験結果データから平均菌数を統計的に算出する方法について、ポアソン分布公式を使いながら解説した。初心者にとっては、第一節で紹介したExcelを用いた平均菌数の算出法から始めることが最も実践的である。

　ポアソン分布は、ランダムに発生する希少なイベントの発生確率をモデル化する際に便利な手法である。すなわち、過去データが少なく、まれにしか検出されない、あるいは極めて低濃度でしか検出されない食中毒菌などの場合に有効である。

　しかし、実際の検査ではさらなる精度を求める場面も多い。その一例が最確数法（MPN法）である。MPN法では、各希釈段階ごとの試験管の陽性率を統計的に統合して解析し、微生物濃度をより正確に推定する。この方法は、今回紹介した単純な計算式が「全体の陽性率」という平面的なデータを扱うのに対し、希釈ごとの陽性・陰性データを多次元的に解析する点が特徴である。ただし、MPN法は計算が非常に複雑であり、統計的知識や専門的なスキルが求められる。そのため、一般的な食品微生物管理者が詳細な理論や計算方法を理解する必要はない。現場では通常、あらかじめ計算されたMPN表を用いて結果を確認するだけで十分である。この手法の理論的背景を深く理解することは、むしろプロフェッショナルの領域であり、専門家が取り扱うべき内容といえる。

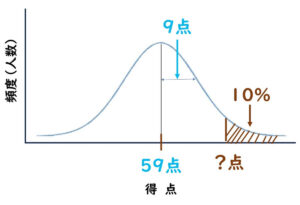
　一方で、検査対象が多く、大量のデータが蓄積されている状況では、ポアソン分布よりもさらに詳細な分布モデルを活用することが有効となる。その一つが対数正規分布である。これは、データがばらつきや偏りを持つ場合や、濃度の分布が広がりを持つ場合に特に有効であり、標準偏差や信頼区間といった要素を解析に活用する。こうした解析手法は、食品微生物の管理基準や予測モデルを設計する際に重要な役割を果たし、ICFMS（International Commission on Food Microbiology and Specifications）の考え方にも深く関わっている。

　次回の記事では、ポアソン分布が希少イベントに適している一方で、対数正規分布がどのように大量データを解析する際に有効かについて、具体的な事例とともに解説する予定である。また、このような分布モデルが食品微生物管理の国際的な標準においてどのように活用されているかについても触れていく。読者の皆さんには、ぜひ次回も楽しみにしていただきたい。