食品の微生物検査の目的を正しく理解し、その精度について知っておくことは重要だ。では、微生物検査ではどれくらいの確率で正しく汚染食品を検出できているのだろうか? 例えば、汚染率10%の食品サンプルをn=3で検査した場合に、すべて陰性と判断してしまう確率は? あるいは、汚染率10%の食品サンプルを95%の精度で検査するためには、いくつのサンプルを分析すればよいのか?
こうした確率の計算には「二項分布」という考え方が使われる。 しかし、「二項分布」と聞くと難しそうに感じるかもしれない。だが心配はいらない。実は、この考え方は くじ引き にたとえると、とても直感的に理解できる。
本記事では、これらの計算を 自分でExcelを使って行えるようになる ことを目指し、順を追ってわかりやすく解説する。数学が苦手な人でも大丈夫! 読み進めれば、食品の微生物検査の精度を確率的に理解する力 が身につくはずだ。
まずは基本的な問題から理解していこう
問題:100枚のくじ引きのうち10枚が当たりくじだった場合(当たり率10%)、10枚のくじ引きを購入した場合どうなるか?

残念ながら10枚ともはずれになる場合もある。

10枚ともハズレくじになる確率は35%である。

小学校から算数や数学が苦手だった場合には、確率という言葉が出ただけで、逃げ出してしまうかもしれない。

しかし、これはそんなに難しくない計算だ。順番に考えてみよう。

今例えば、10枚のカードのうち1枚が当たりくじだったとしよう。ここで1枚だけカードを引いた場合に外れる可能性はどうなるか?これはほとんどの人が、感覚的に理解できるだろう。外れる確率は90%だ。

では2枚のカードを同時に引いた場合にはどうなるか?その確率は0.9×0.9=0.81となる。2枚カードを引くので、はずれカードを引く確率は1枚より下がる。
どのぐらい下がるかといえば、1枚でハズレを引く確率×もう1枚でハズレを引く確率と考えればよい。すなわち、
0.9×0.9=0.81(81%)
となる。

では3枚カードを引けばどうなるか。同じ考え方で0.9×0.9×0.9=0.73(73%)となる。

同じ計算で10枚カードを引いた場合の計算は0.910=0.35なる注)。すなわち35%の確率ですべてを外してしまうことがわかる。

つまり、
- 外れる確率=外れくじの存在割合引いた回数
という計算をすれば良い。

確率計算の近似と正確な計算の違い
上記計算は、正確には、カードを一枚引くたびに残りのカード数が変わり、それに伴って当たりくじを引かない確率も変化する。すなわち、外れる確率は、最初は90/100、次に89/99、そして88/98という具合に計算する必要がある。

しかし、サンプルの数が非常に多い場合、母数の変化は無視できるほど小さい。このため、各サンプルで外れ確率を一律に0.9として計算し、複数サンプルを分析する際には単純に0.9 × 0.9 × 0.9...と計算していくことができる。サンプル数や試行回数が少なく、それによって全体の確率が顕著に変動する場合には、正確な確率計算が必要である。しかし、サンプル数が非常に多い場合には、確率の変動が非常に小さいため、0.9のような一定の値で計算を近似することが許容される。このような近似は、特に大規模なデータセットを扱う統計分析や確率計算において便利だ。本記事で後述する微生物検査の場合がこれに該当する。

食品の微生物検査に当てはめる
以上が理解できれば、食品微生物検査での偽陰性率を出すことも簡単だ。
偽陰性率の計算
さて、ここまでの説明を見て、「これは確率の話だな」と感じた人もいるかもしれない。実際、このような 「成功」か「失敗」かを繰り返し試行する状況」 では、統計学でいう 二項分布 という考え方が使われる。
二項分布とは、「ある試行を何回も繰り返したときに、特定の結果が出る確率」を求めるための分布である。例えば、コイン投げで表が出る確率が 50% だとして、10 回投げたときに 7 回表が出る確率を求めるときに使うのが二項分布だ。
くじ引きの例でも、 「10% の当たりくじが入った箱から 10 回引いたときに、1 枚も当たらない確率」 を求めることは、まさに二項分布の考え方に基づいている。
この考え方は、微生物検査においても 「一定の割合で汚染されたサンプルが存在する中で、n個のサンプルを抜き取ったとき、すべて陰性(非検出)となる確率」 を求める際に使われる。つまり、「偽陰性率の計算」 は、「10%の当たりくじが入った箱から10回引いて、1枚も当たらない確率」を求めるのと 本質的に同じなのだ。
どちらも統計学で「二項分布」と呼ばれる考え方に基づいている。
くじ引きの計算と同じ
問題:全体の20%のサンプルでサルモネラ菌の汚染がある(汚染率20%)サンプルを想定しよう。今、3つのサンプルの抜き打ち検査をした場合に、サルモネラ非検出の結果を判定してしまう確率は?
日常的にはこのようなことはあまり考えず、会社で昔から引き継がれているマニュアルに従って、1サンプルとか3サンプルを分析している場合も多いのではないだろうか。

上のくじ引きの計算とと同じ理屈で食品微生物検査も考えることができる。

すなわち偽陰性を出す確率は、(1-0.2)3=0.83=0.51
51%の確率で偽陰性を出してしまう。つまりこのような検査を行ってロットを出荷した場合には、2回の検査にに1回は汚染事故を起こすことになる。

さらに、例えばサルモネラ菌の汚染率が1%だった製品を想定してみよう。思いっきり頑張って30サンプルを分析してみよう。この場合の陰性確率は?
(1-0.01)30=0.9930=0.74
残念ながら30サンプルを分析しても、74%の可能性で汚染事故を起こすことになる。

このような計算を行っていくと、食品の微生物検査のもつ意味に疑念が生じる人もいるかもしれない。
実際のところ、食品微生物検査の結果を過信するよりは、このような計算を行うことによって、自分たちに行っている検査の精度を正しく理解しておくことは重要だ。
では、n数の少ない微生物検査は全く意味がないのか?
n数が少なくても、微生物検査を行う一つの意味は、食品工場で製品の異常事態を把握するという意味も持っている。

上の計算は、製品中での汚染菌の分布率が低い場合での話である。

食品工場では、例えば、微生物汚染された調味液とか、あるいは食品工場の特定の箇所のバイオフィルムなどから、汚染菌が製品全体に分布してしまうような事故もありうる。このような事故に関しては、例えn数が少なくても、製品のロット検査により、異常事態を検出することができる。
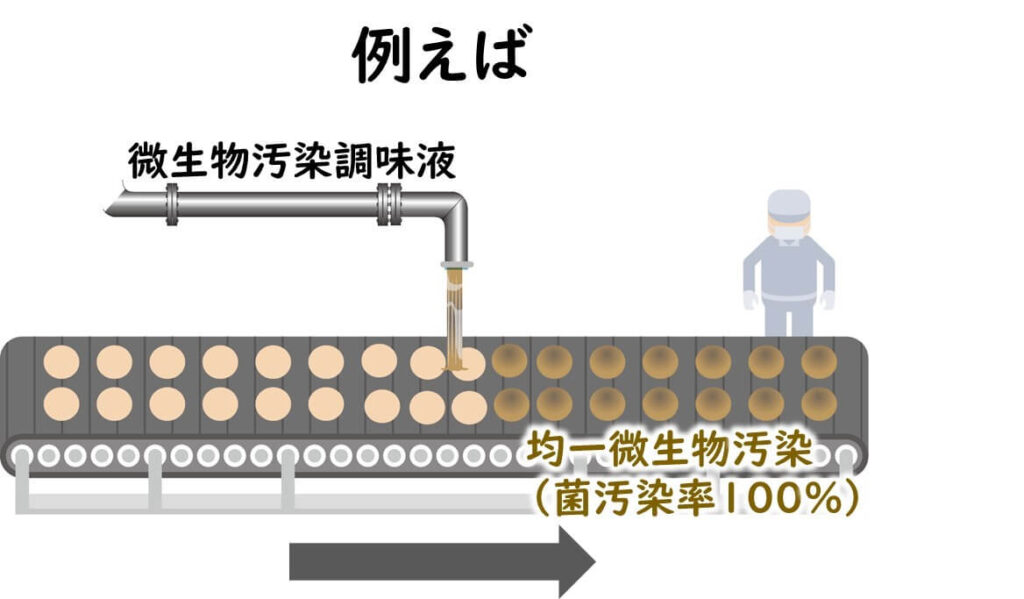
- 汚染率が90%であった場合、たとえ、1サンプルのみの分析でも
(1-0.9)1=0.11=0.1
すなわち、90%の確度で、汚染事故を検出できる。3サンプル分析なら
(1-0.9)3=0.13=0.01
すなわち、99.9%の確度で、汚染事故を検出できる。

いずれにしても、食品微生物の抜き打ち検査において、その結果を過信しないように、不均一分布サンプルの事を念頭において、日常的に微生物の検査結果を考えるべきだということだ。
食品中における微生物の分布は不均一である場合と均一である場合、また分布率が高い場合、低い場合など、いろいろなケースが想定できる。従って、これらの状況をよく自分たちの工場の製品にあてはめて、微生物検査の結果を考えていく解釈力が重要である。

エクセル計算はビデオで分かりやすく説明
ところで以上の計算をエクセルで計算してみよう。これについては、下のビデオをご覧いただきたい。

95%精度で分析するには何サンプル必要なの?
それでは上の計算とは逆に、一定の偽陰性率でで結果を出すために何サンプル分析したらいいのかを計算してみよう。例えば、codexなどでは、正しい検査の偽陰性確率は5%である。すなわち、95%の精度で検査することが求められている。

計算の考え方は、これまで述べてきた考え方と変わらない。ただ問題は求める解の部分が指数になっていることだ。 下記の式でサンプル数を逆算するのは、小学校までの算数では、難しそうだ。
- 外す割合=(1-分布率)サンプル数

log計算が必要だけど基礎理解だけで大丈夫
これを計算式で出すにわlog計算の理解が必要となる。

高校を卒業してからlog計算などとは無縁の生活を送っている人も多いのではないだろうか。

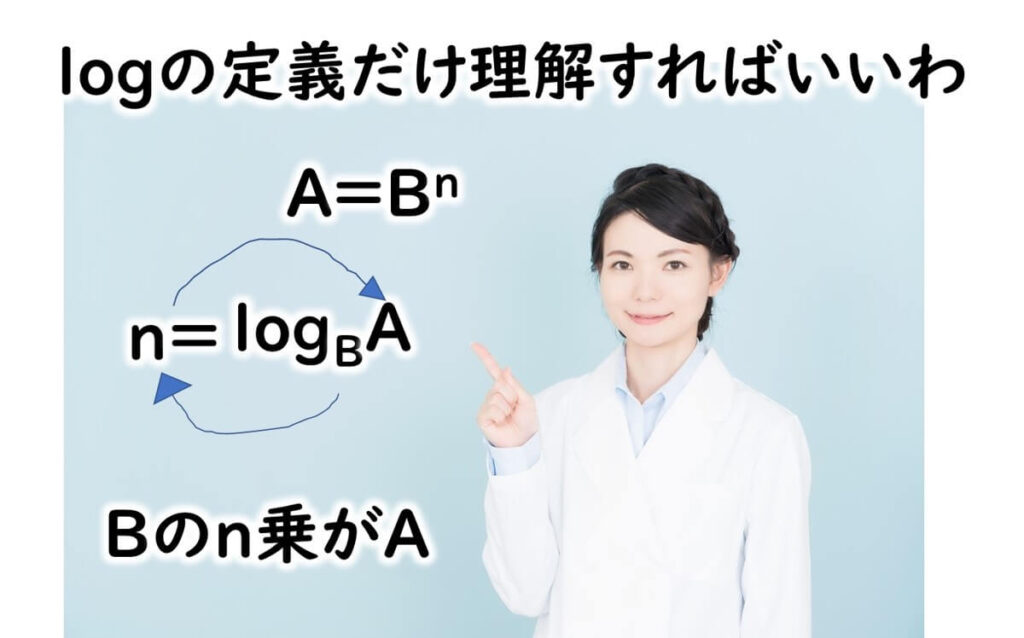
しかし、ここでは難しい計算をするわけではない。logの定義だけを理解すればよい。 Bという数字があって、それをA乗した場合にnになると考える。
A=Bn
この場合のlog記号であらわすと3者の関係は次のとおりとなる。
n=logBA
このlog式では、「Bのn乗がA」という意味を表していると考えればよい。
ここでnを求めたければlogBAをExcelで計算させればよい。手計算では無理なので、Excelを使う。
この関係を微生物の検査で置き換えると次のとおりになる。
サンプル数=log(1-汚染率)偽陰性確率

エクセル計算はビデオで分かりやすく説明
あとは、log(1-汚染率)偽陰性確率をExcelで計算させるだけでよい。Excel計算については、わかりやすくビデオで説明したのでご覧頂きたい。

なお上のビデオで説明しているように、このエクセル計算さえできればたとえば次のようなこともすべて理解できる。
- 輸入サンプル監視をするために、衛生監視員にモニタリング検査を行う場合のサンプル数の検出法(厚生労働省)
日本では、食品を輸入する際、年間計画に基づき食品衛生監視員によるモニタリング検査が実施されている。この際、検査のサンプル数は、輸入量、過去の違反実績、食品の特性などを考慮し、厚生労働省が統計的手法に基づいて決定している。 この考え方は、二項分布を用いた統計的手法に基づいており、国際的にはCODEXの考え方とも整合性がある。つまり、日本の食品衛生によるモニタリング検査のサンプル数の決定も、本記事で照会している統計的手法によるものである。

- 国際的な専門家が論文中で用いる微生物検査精度の議論の理解
例えば、国際食品微生物規格委員会(ICMSF )の議長(2022年5月現在)、ツヴィエタリング(Zwietering)博士の論文では、次のような議論をディスカッションで展開している。
「仮にロット内の微生物汚染の割合がが3.2%であると仮定した場合、ハム製品の不良品を95%の確率で検出することを保証するには、92個(c=0、n=92、25g中非検出検査)のサンプリング計画が必要。その根拠式は
Pdetect(n,c = 0, Pdefective)=1-(1-Pdefective)n」
この式も、記事内で説明してきた二項分布の考え方に基づいた計算である。
一見、専門家による難解な数式に見えるが、この式もよく見ると上述のビデオで説明している方法を実行しているに過ぎないことがわかる。
※ツヴィエタリング(Zwietering)博士の論文時代の内容説明については別記事でまとめていますので、ご覧ください。
出荷時の食品の微生物検査はどこまで役立つの?

結論(食品の微生物検査においては、その目的と精度を正しく理解する)
食品サンプルの微生物検査を行う場合には、その目的と精度を正しく理解しておくことが必要である。特に、次の3点を常に意識しておくことが重要である。
- 食品中における汚染菌の分布割合(これまでの経験値などから判断)
- 所定のサンプル数で検査した場合の偽陰性率(二項分布に基づく計算)
- 95%の精度で検査を行いたい場合の必要なサンプル数(二項分布に基づく計算)
このように、微生物検査におけるサンプル数と精度の関係は、二項分布 に基づく統計的な考え方を利用することで、科学的に説明できる。したがって、食品検査を行う際には、「この検査方法でどの程度の確率で汚染を見逃す可能性があるのか」を統計的に理解し、必要なサンプル数を適切に設定することが重要である。


